Discontinuous Galerkin Approximations to Elliptic and Parabolic Problems with a Dirac Line Source

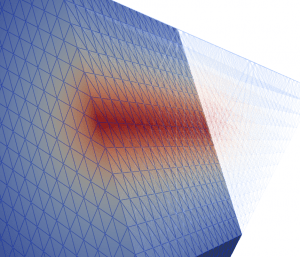Modeling tissue perfusion as blood flow through a porous medium can be challenging since the geometry and the network of these blood vessels are complex. We consider the vessels as one- dimensional fractures embedded in the three-dimensional tissue. In this case, a Dirac measure concentrated on the one-dimensional subdomain is used as a function of the blood pressure in the vessel leading to a coupled 1D-3D problem for the pressure in the tissue and the vessels.